Creation Science Explained
How to put the 'Paleo' in Paleoclimatology: Isotopic Records from Speleothems
By Jonathan Baker, M.S. Geology
Caves are perhaps the most fascinating recorders of Earth's recent climate. Though not the most popular proxy—being stuck in a world of paleoclimatology where tree rings and ice, lake, and marine cores make all of the headlines—caves have the potential to record rainfall and soil data at high resolution for thousands of years. The results are not only locked away in dark rooms, safe from the elements, but are contained within some of the most beautiful rock formations known to us: speleothems.
And that is why we take hammers to them, saw them in half, and mount them on a micro-drilling stage in the isotope geochemistry lab.
Paleoclimate records from stalagmites
By way of preface, I am slightly biased in my attitude, because I've spent the past year analyzing isotopic records from stalagmites around North America. But if you were to consider my position for a moment, I don't think you would disagree. Consider, for example, how a cave forms. Precipitation (or spring meltwater) trickles down through a carbonate aquifer, picking up metal cations (like calcium) and bicarbonate anions along the way. Steady drips of groundwater quickly lose their carbonate concentration to the cave atmosphere by CO2-degassing as they hang from the cave roof (or from stalactites). When the drip hits the floor, further degassing initiates the precipitation of aragonite or calcite (CaCO3). Give the process tens to hundreds to thousands of years, and you have a stalagmite with concentric laminae that reach toward the apex.
As it turns out, the carbon and oxygen isotopic chemistry of the laminae depends primarily on rainfall source and amount, as well as soil activity. We can test these hypotheses by comparing isotopic records from very recently formed stalagmites with human/instrumental climate records, or by comparing the isotopic chemistry of rainwater to dripwater to aragonite in stalagmites over several years. In general, oxygen isotopes are depleted in 18O (heavy oxygen) during wet periods and enriched in 18O during dry periods, but the source of precipitation also plays a role (high vs. low latitude; Atlantic vs. Pacific). Therefore, speleothem records from North America record not only rainfall amount, but migration of the Gulf Stream, El Niño cycles, and other multidecadal oscillations.
Depending on the residence time of the aquifer (i.e. how long, on average, the water takes to get from rainfall to 'cave'-fall), the groundwater will mix thoroughly with that from the past month to the past several years. This means that isotopic inputs from rainfall represent a weighted average for that time interval—good news for the paleoclimatologist. Also, most carbonate ions in groundwater are dissolved within the upper soil horizons during the wet season, so one may track soil processes as well.
Both the hydrological and geochemical processes behind speleothem formation are now very well understood. With few exceptions, stalagmites have been proven faithful proxies of climate. If the sampling process were not so destructive, I believe they would also gain some popularity.
High-resolution age dating of speleothems: answering the 'when' of cave formation
Understanding the climatic significance of isotopic ratios in stalagmites is great, but unless we know when each laminae formed, the records are quite useless. So how does one discern the 'paleo' in paleoclimate? If you've ever had the opportunity to visit a cave set up for guided tours (Cave of the Winds, Colorado and Timpanogos Cave, Utah are on my list), the tour guide likely pointed out a speleothem that had been measured over time: "You see, 50 years ago, this guy was 5 cm shorter! So stalagmites grow about 1 mm per year, and since now it's 105 cm tall, it must have been growing for...1,050 years!"
This approach is simple and intuitive, and in some cases may provide a decent approximation of stalagmite growth. But the fact is, the rate of growth for individual stalagmites can vary over time, due to fluctuations in climate. For example, high amounts of rainfall and soil activity can promote speleothem growth. Low ambient CO2 and high ambient temperature in the cave can also promote growth by increasing the rate of precipitation in each drop. Since we know all of these factors will change over the life of a speleothem, we need a more precise method of dating.
Unfortunately, the popular notion that stalagmite growth-rates are simply extrapolated, like above, has caused young-Earth critics to focus on examples of rapid stalactite growth—some rather odd—to make that case that limestone caves are compatible with a young-Earth, Flood model. But the arguments typically go like this: we know that speleothems can form rapidly under favorable conditions; therefore, all speleothems formed rapidly under favorable conditions. The informal logical fallacy is rarely challenged, because few people are familiar with actual method used to date speleothems.
Uranium-thorium (U-series) dating of speleothems
Most speleothems are originally precipitated as aragonite (calcium carbonate). But like any mineral, the aragonite is bound to contain some impurities. Magnesium, strontium, sodium, barium, and lithium are incorporated in trace amounts. As an aside, the ratio of calcium to these trace elements serves as an independent proxy of climate, occasionally used by ambitious geochemists. One of the most important trace elements, however, is uranium.
Why uranium? Because uranium is radioactive, and decays into thorium at a constant, known rate. By analyzing the current ratio of uranium and thorium isotopes, one can estimate the absolute age of laminae in speleothems. More specifically, the ratio of 234U (parent) to 230Th (daughter) is measured. But the ratio does not change like an hourglass model with time (as in the radiocarbon, K-Ar, and U-Pb systems), since the daughter product is also radioactive, and decays even faster than the parent. Let's take a closer look.
Money matters: a financial analogy
Imagine that you set up a bank account with $1,000 in savings and $0
in checking. Every month, 1% of the savings amount is transferred to
checking, but 5% of the checking amount is...donated to charity. In
this scenario, the money in savings represents 234-Uranium, and the
money in checking represents 230-Thorium. Both accounts are
constantly decaying at a constant rate, unique to each account, that
depends on the residual balance. The money spent to charity
represents the daughter product of thorium decay, which is neither
measured in the rock nor this analogy.At the end of the first month, zero dollars are donated to charity, because the checking account has zero dollars available. But 1%, or $10, will be transferred from savings to checking. The new balance: $990 in savings; $10 in checking. So at the end of the second month, 5% of $10, or 50 cents, will be donated to charity, and $9.90 transferred from savings to checking. The new balances: $980.10 in savings; $19.40 in checking. Easy enough?
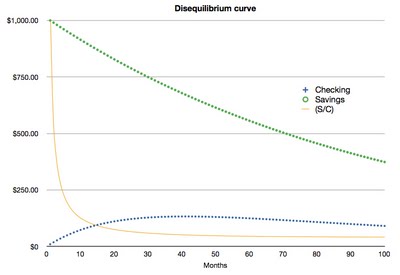
In geology, we actually measure the ratio between the isotopes (i.e. $ in savings divided by $ in checking). If we know the rate of decay (what % is lost each month), and the original balance in at least one of the accounts, we can back calculate the time that has passed since the experiment started. Below, I have plotted the experiment over 100 months:
The yellow line represents the ratio between the two accounts. As you can see, the ratio changes very quickly at first, but eventually flattens out to equilibrium (hence the name "Uranium-Thorium Disequilibrium Dating"). This means that if one were to estimate the time passed based on the current ratio between the accounts, that estimate would be more precise at time = 0–30 months than at time = 30–100 months. Correspondingly, U-Th disequilibrium ages are most precise up to ~500,000 years, after which the change in 234U/230Th is too small to be detected.
Another limit occurs in very young samples, since the mass spectrometer is unable to detect thorium at exceedingly low concentrations. Thus ideal samples are uranium-rich to begin with, and are at least several years to several thousand years old. Personally, I have seen very precise (±1%) age estimates from U-rich samples, however, even between 0 and 100 years old.
Depending on the scientific importance of the sample, and given that each age datum costs ~$500 to analyze, between 2 and 20 U-Th dates are taken along the growth axis. This allows the paleoclimatologist to construct an age model for each speleothem, and attach real ages to isotopic records.
But aren't there a few assumptions involved?
Yes, some assumptions are made. That is how science progresses. But fortunately for us, most of those assumptions can be falsified/verified independently.
1) How do we know the initial ratio of U/Th isotopes? In oxic environments, uranium is fairly soluble and thorium is very insoluble. Since stalagmites form out of dissolved constituents of groundwater, we should expect very little, if any, thorium to be originally present (i.e. $0 in checking).
2) Does this assumption always hold? On the contrary, we expect this assumption never to hold, in the absolute sense. There will always be at least some thorium present. So to account for this, we measure the ratio of 238U to 232Th (two common isotopes). Both isotopes are radioactive, but their half-lives (4.5 and 14.05 billion years, respectively) are much longer than that of 230Th (75,380 years), and may be considered stable on shorter geologic timescales. Using the 238U/232Th ratio, the 232Th/230Th ratio, and the total concentration of uranium, we can estimate the initial concentration of 230-thorium. Typically, this value is insignificant, and will only change the age estimates by a maximum of 1% if left uncorrected. To put this in perspective, imagine that I started the experiment above with $1.50 in checking. In this case, the age estimate would be off by less than a few days.
3) How do we know whether any uranium or thorium was lost since crystallization? In speleothems, this is rarely a concern, since most ages fit very well into a growth model (i.e. they get progressively older along the axis, and result in globally correlated paleoclimate records). But if this assumption were challenged, one could use trace element data, petrography, and cathodoluminescence to test whether recrystallization of the speleothem caused a loss of soluble trace-elements. Also, any loss of uranium is likely to be localized, through microfractures in the speleothem. In this case, model ages taken from those points will show up as anomalous, and result in an unrealistic growth-rate curve. It is simply unreasonable to expect that uranium loss occurred systematically, shifting all the ages by a proportional amount.
4) How do we know the decay rates for both isotopes has remained the same? This is a matter of quantum physics, and a sound one at that. There is no reason to expect decay rates to change. If this were to happen, however, during the life of the speleothem, then the growth model would shift dramatically at a point, making it appear as though the speleothem started to grow many times faster or slower.
Are caves and speleothems consistent with the Flood model?
In short, no. The Flood model must consider modern caves and speleothems as post-Flood features. Even if one were to allow for the unrealistic scenario of accelerated nuclear decay during, the caveat would not apply to speleothems. Since thousands of speleothems have been dated beyond 5,000 years, there remains a significant challenge to young-Earth Flood geologists.
We can also consider speleothem records in the larger climatic context. For example, speleothem records match up very well with ice core records (dated by counting annual layers), marine/lake core records (dated by counting annual layers and radiocarbon methods), and tree ring records (same as above). Thus we have multiple independent methods yielding essentially the same result. Such concordance highly corroborates the use of each method to track the Earth's climate history, and thoroughly falsifies the Flood model.
This article was originally posted by Jonathan Baker on his blog, Questioning Answers in Genesis.
To learn more
about old earth creationism, see
Old Earth Belief,
or check out the article
Can You Be A
Christian and Believe in an Old Earth?
Feel free to check out more of this website. Our goal is to
provide rebuttals to the bad science behind young earth creationism,
and honor God by properly presenting His creation.